Spectral Analysis With Energy Filters
In these series of works, we probe spectral properties of quantum many-body systems with Gaussian energy filters of the form
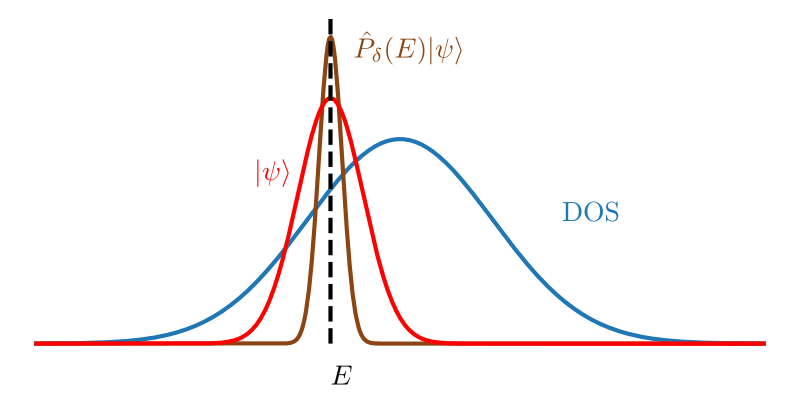
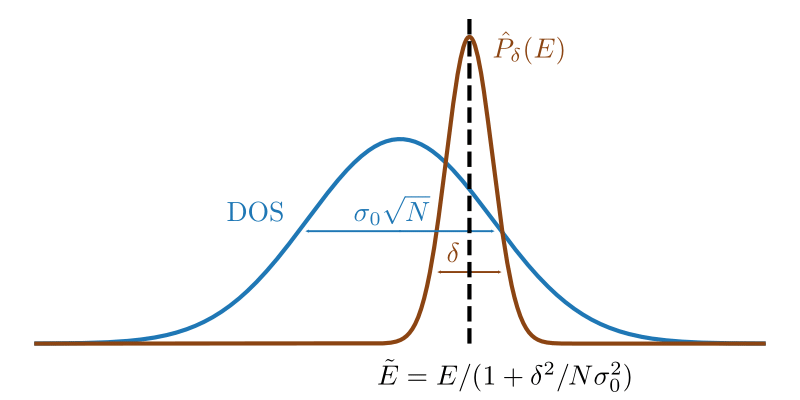
$$ P_{\delta}(E) = \exp\left[ - \frac{(E-H)^2}{2\delta^2}\right]. $$Thermalization probes
[1] Probing Thermalization through Spectral Analysis with Matrix Product Operators
Y. Yang, S. Iblisdir, J. I. Cirac, and M. C. Bañuls
Phys. Rev. Lett. 124, 100602 (2020)[2] Classical algorithms for many-body quantum systems at finite energies
Y. Yang, J. I. Cirac, and M. C. Bañuls
Phys. Rev. B 106, 024307 (2022) (Editor′s suggestion)[3] How thermal is a filtered state?
In preparation.
The microcanonical ensemble at finite energy density plays a central role in many-body physics, enabling the study of long-time dynamics and nonequilibrium phenomena. Unlike canonical ensembles, however, few algorithm previously existed for computing microcanonical properties.
This challenge can be addressed by applying energy filters to the entire Hamiltonian spectrum[1,2]. By suppressing irrelevant eigenstates, such filters yield the microcanonical ensemble \( \rho_E \approx P_{\delta}(E) / \mathrm{tr} \left[ P_{\delta}(E)\right] \). In one-dimensional systems, these filters can be efficiently implemented using tensor networks via Chebyshev or Fourier expansions.
Moreover, applying the filter directly to a quantum state produces a state approximating thermal equilibrium under the eigenstate thermalization hypothesis (ETH)[3].
Measuring Eigenvalue degeneracies
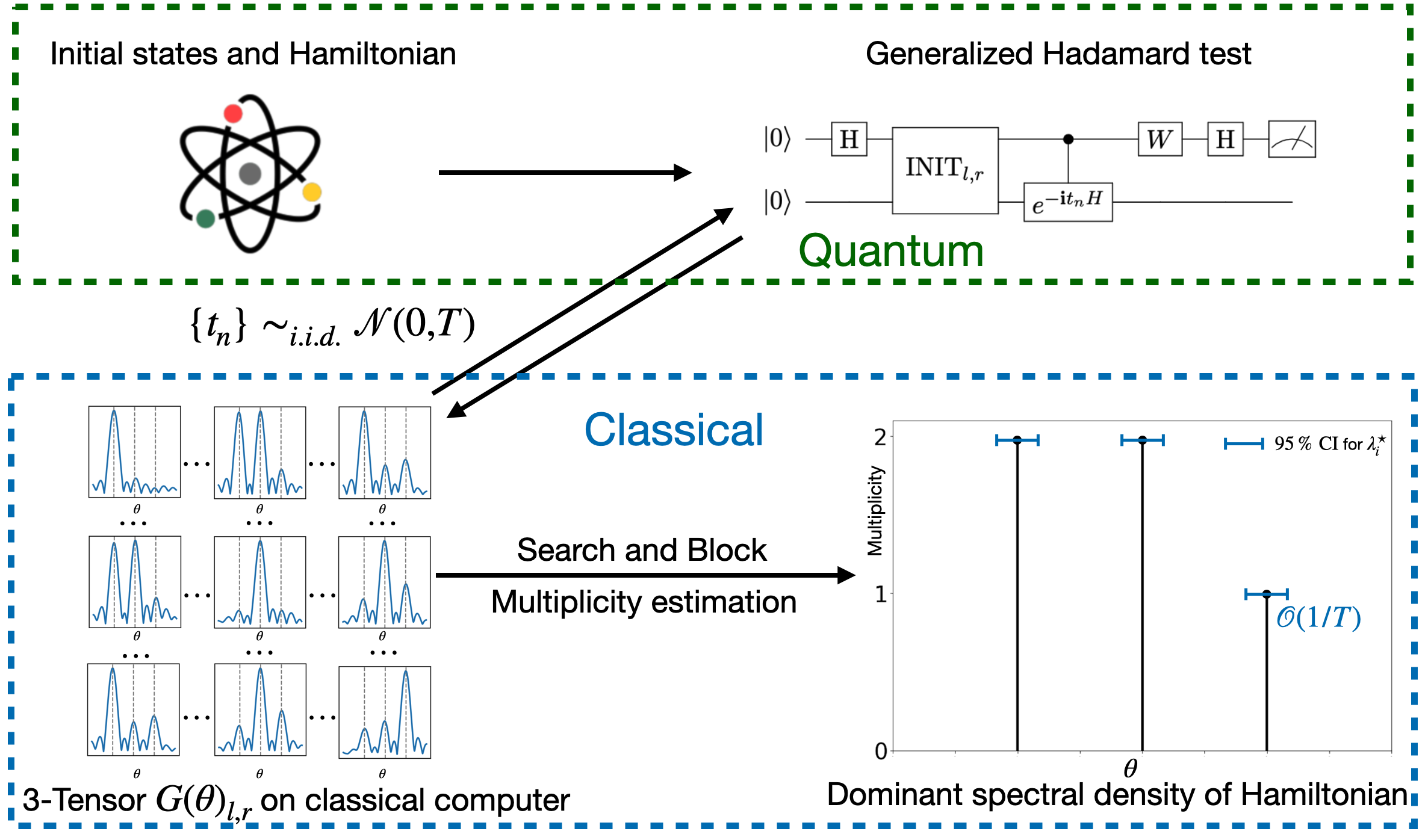
- Quantum Filtering and Analysis of Multiplicities in Eigenvalue Spectra
Z. Ding, L. Lin, Y. Yang, R. Zhang
arXiv:2510.07439 (2025) [quant-ph]
By scanning over different filter centers, one can reconstruct the local density of states of a chosen initial state, thereby estimating the underlying energy eigenvalues. Remarkably, when multiple initial states are available, this approach also enables the estimation of eigenvalue degeneracies, which is missing in conventional quantum phase estimation algorithms.
Related works
- Algorithms for Quantum Simulation at Finite Energies, S. Lu, M. C. Bañuls, and J. I. Cirac, PRX Quantum 2, 020321 (2021)
- Approximating the long time average of the density operator: Diagonal ensemble, A. Çakan, J. I. Cirac, and M. C. Bañuls, Phys. Rev. B 103, 115113 (2021)
- Probing off-diagonal eigenstate thermalization with tensor networks, M. Luo, R. Trivedi, M. C. Bañuls, and J. I. Cirac, Phys. Rev. B 109, 134304 (2024)
- Measuring the Loschmidt Amplitude for Finite-Energy Properties of the Fermi-Hubbard Model on an Ion-Trap Quantum Computer, K. Hémery, et al., PRX Quantum 5, 030323 (2024)
- Quantum Multiple Eigenvalue Gaussian filtered Search: an efficient and versatile quantum phase estimation method, Z. Ding, et al., Quantum 8, 1487 (2024)