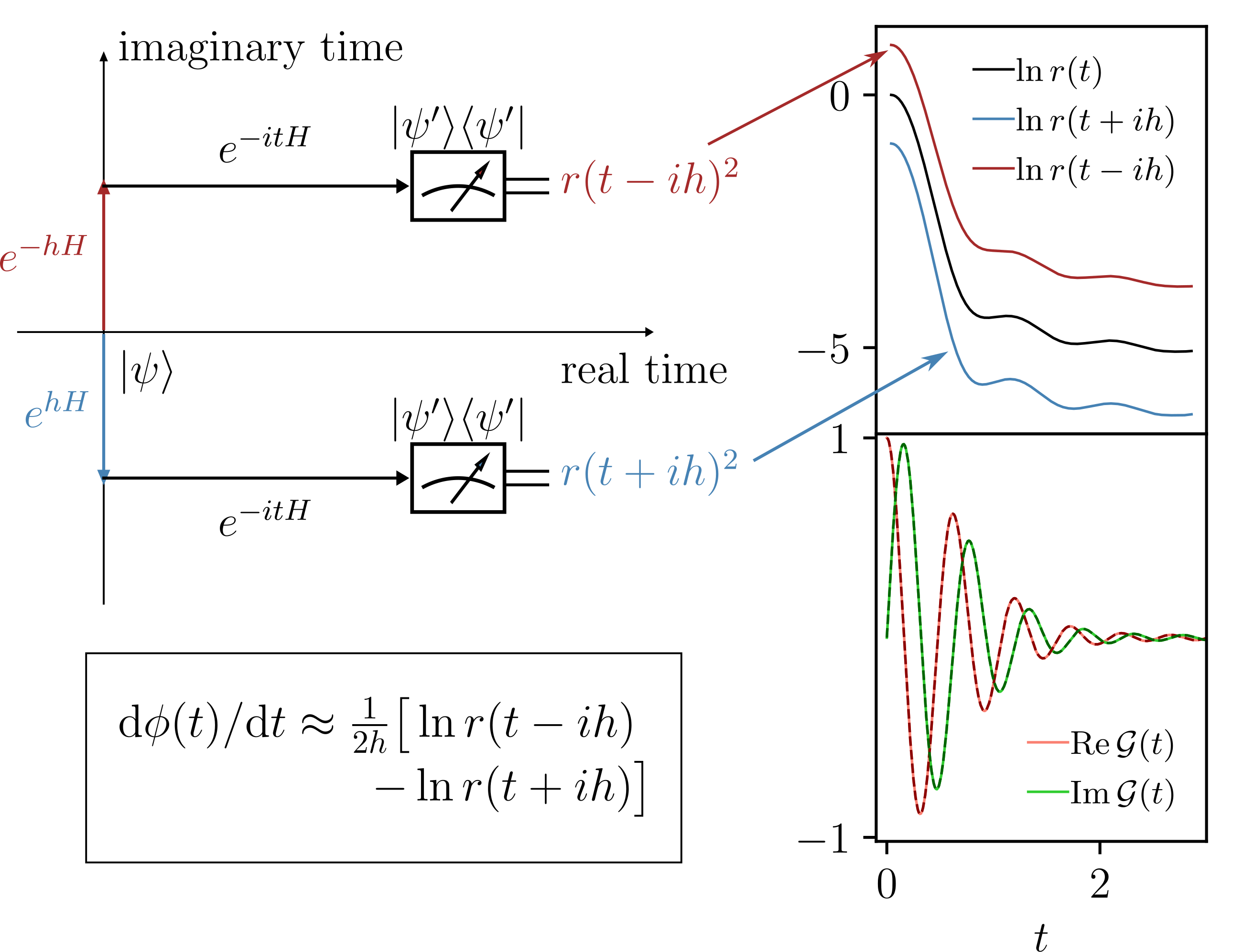
• Phase-Sensitive Quantum Measurement without Controlled Operations
  Y. Yang, A. Christianen, M. C. Bañuls, D. S. Wild, and J. I. Cirac,
  Phys. Rev. Lett. 132, 220601

The Loschmidt amplitude \( \mathcal{G}(t) = \langle \psi^{\prime} | e^{-iH t} | \psi \rangle \) including the complex phase has broad applications in quantum computation, study of quantum chaos and so on. The standard way to extract the phase information is the Hadamard test, which gives rise to large overheads due to the need for global controlled-unitary operations. We introduce a quantum algorithm based on complex analysis that overcomes this problem: no ancillary qubits, no control operations, only time evolution required.

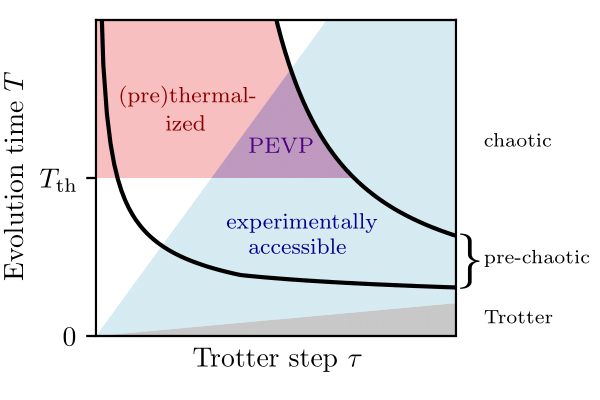
• Simulating Prethermalization Using Near-Term Quantum Computers
  Y. Yang, A. Christianen, S. Coll-Vinent, V. Smelyanskiy, M. C. Bañuls, T. E. O′Brien, D. S. Wild, and J. I. Cirac,
  PRX Quantum 4, 030320

Due to decoherence and noise in current devices, it is currently challenging to perform digital quantum simulation in a regime that is intractable with classical computers. In this work, we propose a practical experimental protocol for probing dynamics and equilibrium properties on near-term digital quantum computers, based on the prethermalization phenomenon and a proposed error mitigation scheme.

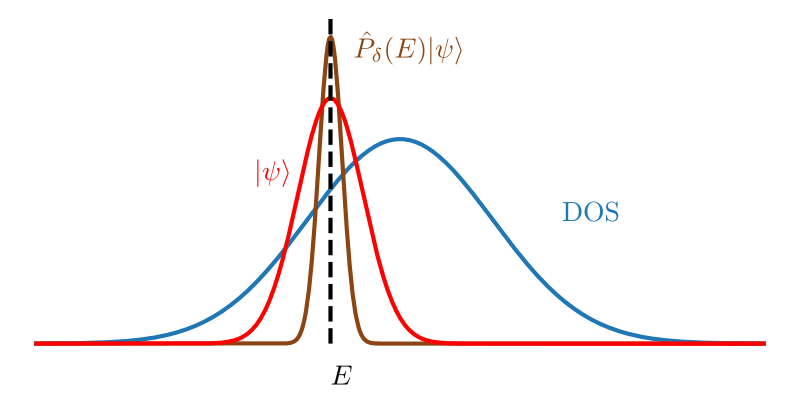
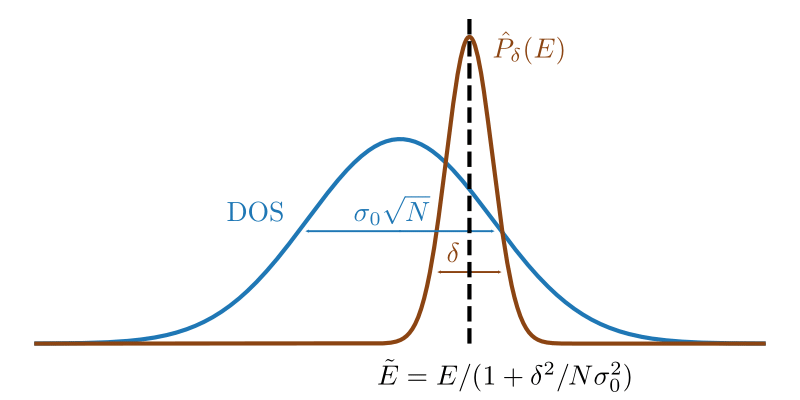
• Probing Thermalization through Spectral Analysis with Matrix Product Operators
  Y. Yang, S. Iblisdir, J. I. Cirac, and M. C. Bañuls
  Phys. Rev. Lett. 124, 100602

• Classical algorithms for many-body quantum systems at finite energies
  Y. Yang, J. I. Cirac, and M. C. Bañuls
  Phys. Rev. B 106, 024307 (Editor′s suggestion)

The microcanonical ensembles at finite energy densities have many applications in many body physics. It enables studying the long time behaviors of given initial states and helps to probe the out-of-equilibrium phenomena. Unlike the canonical ensembles, no standard algorithm previously exists for computing microcanonical ensemble properties.

We develop a technique to solve this problem using energy filters that can be applied to both fixed initial states and the whole spectrum. A (Gaussian) filter \(P_{\delta} (E) = \exp[-(E-H)^2 / 2\delta^2]\) as a energy projector can filter out irrelevant energy eigenstates and thus obtain the microcanonical ensemble. Such filters can be efficiently implemented with tensor networks in one-dimensional systems, by expanding it with the Chebyshev or Fourier series.